Factors of 30 (Explained By Experts)

Factors of 30

The factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30. These are the whole numbers that divide 30 exactly, including its prime factors, which are 2, 3, and 5. You can use the division method, listing method, prime factorization, and factor tree method to find the factors of 24.

Steps of Finding Factors of 30

Here are the steps to find the factors of 30:

Write down the number you want to find the factors of, in this case, 30.
Find two numbers that multiply to give you 30. Start with 1 and 30, and then try 2 and 15, 3 and 10, and 5 and 6.
If you find a pair of numbers that multiply tp 30, write them down as factors. For example, if you try 2 and 15, you can write down “2, 15” as factors of 30.
Keep going until you have found all the factors of 30. In this case, the factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30.
Alternatively, you can use the prime factorization method to find the factors of 30. First, find the prime factors of 30, which are 2, 3, and 5. Then, write down all the possible combinations of these prime factors. For example:

2 x 3 x 5 = 30
2 x 15 = 30
3 x 10 = 30
5 x 6 = 30
These are all the factors of 30.

What is the importance of factorization in Mathematics?

Factorization is an important concept in mathematics for many reasons, including:

Simplification of fractions: Factorization is used to simplify fractions by reducing the numerator and denominator to their lowest terms. This helps in making complex calculations easier.

Solving equations: Factorization is used to solve equations by factoring the expression on one side of the equation and then finding the roots of the resulting factors. This technique is used in algebra and calculus to solve equations.

Prime numbers: Factorization is used to determine whether a number is a prime or composite number. Prime numbers are those that have only two factors, 1 and itself. All other numbers are composite numbers, and can be factored into a product of prime factors.

Cryptography: Factorization plays a vital role in cryptography, which is the science of encoding and decoding secret messages. In particular, factoring large numbers is used in public key cryptography to encrypt and decrypt messages.

Coding theory: Factorization is also used in coding theory to create error-correcting codes that are used in digital communications.

Overall, factorization is a fundamental concept in mathematics with numerous applications in different fields. It helps in understanding the properties of numbers and shapes the way we interact with them.

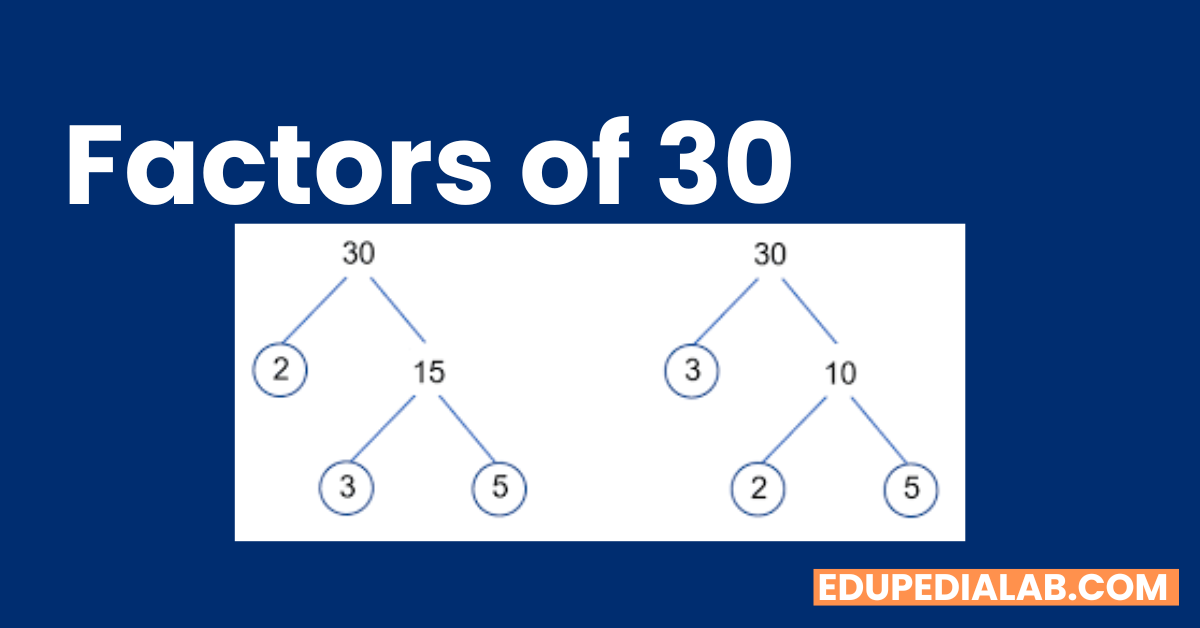
Is it possible to calculate the factorization of 30 by the factor tree method?

Yes, it is possible to calculate the factorization of 30 by the factor tree method. Here are the steps:

Write down the number 30 at the top of the page.
Find two factors of 30. The prime factors of 30 are 2, 3, and 5, so you can start by dividing 30 by 2 to get 15.
Write 2 and 15 as the first two branches of the factor tree, and repeat the process with 15. Divide 15 by 3 to get 5.
Write 3 and 5 as the next two branches of the factor tree. 5 is a prime number, so we have completed the factorization.
Write down all the branches of the factor tree from top to bottom: 2 x 3 x 5 = 30.
These are all the factors of 30: 1, 2, 3, 5, 6, 10, 15, and 30.
So, by using the factor tree method, we can easily find the prime factors and all the factors of 30.

Summary

Factorization of 30 involves finding the factors of the number 30, which are the whole numbers that divide 30 exactly. The prime factors of 30 are 2, 3, and 5. By multiplying these prime factors together, we get 30. The factorization of 30 can be found by using various methods such as listing the factors, prime factorization, or factor trees. The factors of 30 include 1, 2, 3, 5, 6, 10, 15, and 30, and they are useful in many areas of mathematics and science, including simplification of fractions, cryptography, and coding theory.